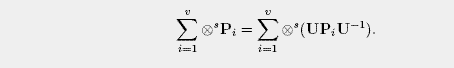Quantum Designs - Definitions
A quantum design is a set D = {P1, ..., Pv} of
orthogonal d x d projection matrices.
- D is said to be regular if there exists an
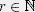 such that such that
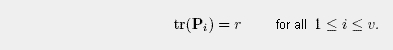
- The degree s of D is given by the cardinality of the set
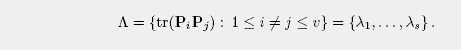
- A subset of D is an orthogonal class,
if its projections are pairwise orthogonal.
If the sum of all its projections adds up to the identity matrix,
the orthogonal class is said to be complete.
A quantum design is called resolvable if it can be written as a disjoint
union of complete orthogonal classes.
- A regular resolvable quantum design with degree 2
will be called an affine quantum design.
- Let G be an irreducible group of unitary d x d matrices.
Then D is a quantum t-design with respect to the group G
if the following equation holds for all matrices
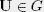 and all
and all 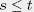 : :
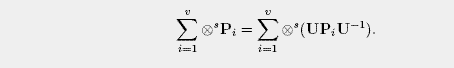
For classical=commutative quantum designs (out of pairwise commuting projections) these
definitions correspond to those of combinatorial design theory (the terminology is as in the book
Design Theory, by T.Beth, D.Jungnickel, H.Lenz).
The assignment goes via the 0/1 diagonal entries of the simultaneously diagonalized
projection matrices taken as incidence functions of subsets of a set of
d elements. The appropriate group G is given by the d x d permutation matrices.
|
| Diese Seite ist nur auf Englisch verfügbar |
|

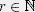 such that
such that 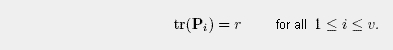
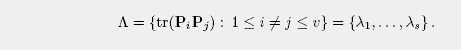
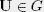 and all
and all 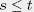 :
: